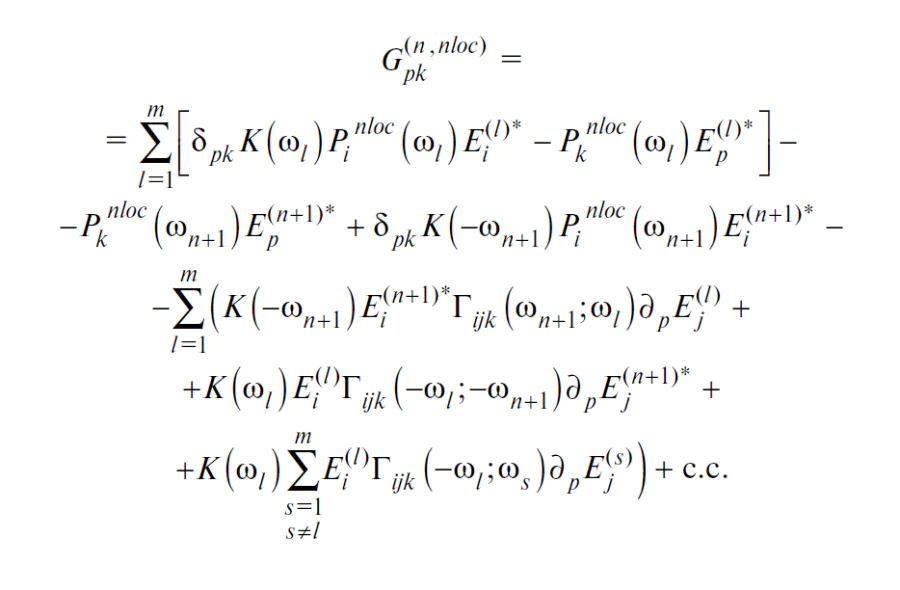Home / Publications / ENERGY, MOMENTUM, AND ANGULAR MOMENTUM OF ELECTROMAGNETIC FIELD IN A MEDIUM WITH NONLOCAL OPTICAL RESPONSE UNDER FREQUENCY-DEGENERATE NONLINEAR WAVE INTERACTION

ENERGY, MOMENTUM, AND ANGULAR MOMENTUM OF ELECTROMAGNETIC FIELD IN A MEDIUM WITH NONLOCAL OPTICAL RESPONSE UNDER FREQUENCY-DEGENERATE NONLINEAR WAVE INTERACTION

P. S. Ryzhikov 1 *
P. S. Ryzhikov
* ryzhikov.ps14@physics.msu.ru
, 
V. A. Makarov 1
V. A. Makarov
10.31857/S00444510240202e2
Published 2023-10-17
Article , Volume 165, Issue 2, 142-158
Share
Cite this
GOST
 | 
Cite this
GOST Copy
Ryzhikov P. S., Makarov V. A. ENERGY, MOMENTUM, AND ANGULAR MOMENTUM OF ELECTROMAGNETIC FIELD IN A MEDIUM WITH NONLOCAL OPTICAL RESPONSE UNDER FREQUENCY-DEGENERATE NONLINEAR WAVE INTERACTION // Journal of Experimental and Theoretical Physics. 2023. Vol. 165. No. 2. pp. 142-158.
GOST all authors (up to 50) Copy
Ryzhikov P. S., Makarov V. A. ENERGY, MOMENTUM, AND ANGULAR MOMENTUM OF ELECTROMAGNETIC FIELD IN A MEDIUM WITH NONLOCAL OPTICAL RESPONSE UNDER FREQUENCY-DEGENERATE NONLINEAR WAVE INTERACTION // Journal of Experimental and Theoretical Physics. 2023. Vol. 165. No. 2. pp. 142-158.
RIS
 | 
Cite this
RIS Copy
TY - JOUR
DO - 10.31857/S00444510240202e2
UR - https://jetp.colab.ws/publications/10.31857/S00444510240202e2
TI - ENERGY, MOMENTUM, AND ANGULAR MOMENTUM OF ELECTROMAGNETIC FIELD IN A MEDIUM WITH NONLOCAL OPTICAL RESPONSE UNDER FREQUENCY-DEGENERATE NONLINEAR WAVE INTERACTION
T2 - Journal of Experimental and Theoretical Physics
AU - Ryzhikov, P. S.
AU - Makarov, V. A.
PY - 2023
DA - 2023/10/17
PB - Nauka Publishers
SP - 142-158
IS - 2
VL - 165
ER -
BibTex
 | 
Cite this
BibTex (up to 50 authors) Copy
@article{2023_Ryzhikov,
author = {P. S. Ryzhikov and V. A. Makarov},
title = {ENERGY, MOMENTUM, AND ANGULAR MOMENTUM OF ELECTROMAGNETIC FIELD IN A MEDIUM WITH NONLOCAL OPTICAL RESPONSE UNDER FREQUENCY-DEGENERATE NONLINEAR WAVE INTERACTION},
journal = {Journal of Experimental and Theoretical Physics},
year = {2023},
volume = {165},
publisher = {Nauka Publishers},
month = {Oct},
url = {https://jetp.colab.ws/publications/10.31857/S00444510240202e2},
number = {2},
pages = {142--158},
doi = {10.31857/S00444510240202e2}
}
MLA
Cite this
MLA Copy
Ryzhikov, P. S., and V. A. Makarov. “ENERGY, MOMENTUM, AND ANGULAR MOMENTUM OF ELECTROMAGNETIC FIELD IN A MEDIUM WITH NONLOCAL OPTICAL RESPONSE UNDER FREQUENCY-DEGENERATE NONLINEAR WAVE INTERACTION.” Journal of Experimental and Theoretical Physics, vol. 165, no. 2, Oct. 2023, pp. 142-158. https://jetp.colab.ws/publications/10.31857/S00444510240202e2.
Views / Downloads
11 / 34

Keywords

nonlinear optics
optical angular momentum
spatial dispersion

Abstract

The expressions for the additional terms to the electromagnetic field energy density, energy flux density, momentum density, momentum flux density, components of angular momentum density and components of anglular momentum flux density tensor in a medium with nonlocality of the n-th order nonlinear optical response are obtained from the Maxwell equations system for the case when the number of the interacting waves with different frequencies is less than or equal to n (frequency-degenerate processes). It is shown that the intrinsic symmetry relations between the components of both local and nonlocal nonlinear susceptibility tensors make it impossible to obtain the correct formulas for the aforementioned fundamental characteristics of the electromagnetic field as a particular case of the already known expressions for these quantities related to the nonlinear interaction of n + 1 waves with absolutely different frequencies if we put some frequencies equal to each other. As an example, we discuss the obtained additional terms caused by nonlocal nonlinear optical response of the medium in cases of self-focusing, second- and third-harmonic generation.

The bibliography includes 33 references.

[1-33]

References

1.
L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics, 8 Electrodynamics of continuous media. (Elsevier, 1984).
3.
L. Campos-Flores, J. L. Jimenez-Ramirez, and J. Roa-Neri, Journal of Electromagnetic Analysis and Applications, 203, (2017)
4.
D. E. Soper, Classical Field Theory. (Dover Publications, 2008). JETP, Vol. 165, No. 2, 2024
5.
S. M. Barnett, Journal of Optics B: Quantum and Semiclassical Optics, 4, S7 (2002).
6.
V. P. Makarov and A. A. Rukhadze, Phys. Usp., 181, 1357 (2011).
7.
S. Stallinga, Phys. Rev. E, 73, 026606, (2006).
8.
O. Yamashita, Optik, 122, 2119 (2011).
9.
V. M. Agranovich and V. L. Ginzburg, Crystal Optics with Spatial Dispersion, and Excitons. (Springer-Verlag, Berlin, Heidelberg, 1965).
10.
P. W. Milonni and R. W. Boyd. Adv. Opt. Photon., 2 , 519, (2010).
11.
C. Heredia and J. Llosa, Journal of Physics Communications, 5, 055003 (2021).
12.
R. Boyd, Nonlinear optics. (Elsevier, 2020).
13.
S. Serulnik and Y. Ben-Aryeh, Quantum Optics: Journal of the European Optical Society Part B, 3, 63 (1991).
14.
G. Moe and W. Happer, Journal of Physics B: Atomic and Molecular Physics, 10, 1191 (1977).
15.
S. A. Akhmanov and S. Yu. Nikitin, Physical Optics. (Nauka, 2004) [in Russian].
16.
S. M. Barnett, Phys. Rev. Lett., 104, 070401 (2010).
17.
A. Willner, H. Huang, Y. Yan, Y. Ren, N. Ahmed, G. Xie, C. Bao, L. Li, Y. Cao, Z. Zhao, J. Wang, M. Lavery, M. Tur, S. Ramachandran, A. Molisch, N. Ashrafi, and S. Ashrafi, Advances in Optics and Photonics, 7, 66 (2015).
18.
A. Trichili, C. Rosales-Guzmán, A. Dudley, B. Ndagano, A. Salem, M. Zghal, and A. Forbes, Scientific Reports, 6, 27674 (2016).
19.
V. D’Ambrosio, E. Nagali, S. Walborn, L. Aolita, S. Slussarenko, L. Marrucci, and F. Sciarrino, Nature communications, 3, 961 (2012).
20.
W. Brullot, M. Vanbel, T. Swusten, and T. Verbiest, Science Advances, 2, e1501349 (2016).
21.
P. Polimeno, A. Magazzu`, M. Iatì, F. Patti, R. Saija, C. Boschi, M. Donato, P. Gucciardi, P. Jones, G. Volpe, and O. M. Marago, Journal of Quantitative Spectroscopy and Radiative Transfer, 218, 131 (2018).
22.
Y. Tian, L. Wang, and G. Duan, Optics Communications, 485, 126712 (2020).
23.
M. Padgett and R. Bowman, Nature Photonics, 5, 343 (2011).
24.
S. Franke-Arnold, L. Allen, and M. Padgett, Laser and Photonics Review, 2, 299 (2008).
25.
A. Yao and M. Padgett, Advances in Optics and Photonics, 3, 161 (2011).
26.
M. Ritsch-Marte, Philosophical Transactions of The Royal Society A Mathematical Physical and Engineering Sciences, 375, 20150437 (2017).
27.
P. S. Ryzhikov and V. A. Makarov, JETP, 162, 45 (2022).
28.
P. S. Ryzhikov and V. A. Makarov, Laser Physics Letters, 19, 115401 (2022).
29.
Y. R. Shen, Principles of nonlinear optics. (Wiley, 1984).
30.
P. S. Ryzhikov and V. A. Makarov, Laser Physics Letters, 20, 105401 (2023).
31.
S. V. Popov, Yu. P. Svirko, and N. I. Zheludev, Susceptibility tensor for nonlinear optics. (Optics and optoelectronics series. Institute of Physics Publishing, Bristol and Philadelphia, 2015).
32.
Y. P. Svirko and N. I. Zheludev, Polarization of light in nonlinear optics. (Wiley, 1998).
33.
P. S. Ryzhikov and V. A. Makarov, Laser Physics Letters, 19, 035401 (2022).